Insurance pricing is a complex process where companies determine premiums based on various risk factors such as age, health, income, claims history, and lifestyle. However, the exact pricing models used by insurers are proprietary, making it difficult for customers and businesses to understand premium calculations.

In this project, we build a machine learning model using EDA, feature engineering, and XGBoost to predict insurance premium amounts. By mimicking the insurer’s pricing strategy, our goal is to uncover key factors affecting premiums and develop a data-driven premium estimation tool.

Estimate Insurance Premiums

To run the project, we follow the essential steps of a data science project as follows.

1. Problem Definition and Business Understanding

Insurance companies assess risk factors to price policies, but customers often lack transparency on why they are charged certain premiums. A predictive model can:

Our goal is to predict the insurance premium amount a customer would be charged based on their attributes using machine learning models. The model will identify the most important risk factors and help in estimating premiums for new customers.

2. Dataset Description

The dataset train.csv includes various customer attributes that influence premium pricing. Key features include:

Numerical Features

Categorical Features

Target Variable

3. Data Exploration Analysis (EDA)

Load Dataset

# All required libraries are imported here
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_log_error
from xgboost import XGBRegressor
import scipy.stats as stats
import math
from scipy.stats import kruskal

# Load Dataset
file_path = "train.csv"  
df = pd.read_csv(file_path)

print(f"Data shape: {df.shape}")
print(df.head())
print(df.info())

Output:

Data shape: (1200000, 21)
   id   Age  Gender  Annual Income Marital Status  Number of Dependents  \
0   0  19.0  Female        10049.0        Married                   1.0   
1   1  39.0  Female        31678.0       Divorced                   3.0   
2   2  23.0    Male        25602.0       Divorced                   3.0   
3   3  21.0    Male       141855.0        Married                   2.0   
4   4  21.0    Male        39651.0         Single                   1.0   

  Education Level     Occupation  Health Score  Location  ... Previous Claims  \
0      Bachelor's  Self-Employed     22.598761     Urban  ...             2.0   
1        Master's            NaN     15.569731     Rural  ...             1.0   
2     High School  Self-Employed     47.177549  Suburban  ...             1.0   
3      Bachelor's            NaN     10.938144     Rural  ...             1.0   
4      Bachelor's  Self-Employed     20.376094     Rural  ...             0.0   

   Vehicle Age  Credit Score  Insurance Duration           Policy Start Date  \
0         17.0         372.0                 5.0  2023-12-23 15:21:39.134960   
1         12.0         694.0                 2.0  2023-06-12 15:21:39.111551   
2         14.0           NaN                 3.0  2023-09-30 15:21:39.221386   
3          0.0         367.0                 1.0  2024-06-12 15:21:39.226954   
4          8.0         598.0                 4.0  2021-12-01 15:21:39.252145   

  Customer Feedback Smoking Status Exercise Frequency Property Type  \
0              Poor             No             Weekly         House   
1           Average            Yes            Monthly         House   
2              Good            Yes             Weekly         House   
3              Poor            Yes              Daily     Apartment   
4              Poor            Yes             Weekly         House   

  Premium Amount  
0         2869.0  
1         1483.0  
2          567.0  
3          765.0  
4         2022.0  

[5 rows x 21 columns]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1200000 entries, 0 to 1199999
Data columns (total 21 columns):
 #   Column                Non-Null Count    Dtype  
---  ------                --------------    -----  
 0   id                    1200000 non-null  int64  
 1   Age                   1181295 non-null  float64
 2   Gender                1200000 non-null  object 
 3   Annual Income         1155051 non-null  float64
 4   Marital Status        1181471 non-null  object 
 5   Number of Dependents  1090328 non-null  float64
 6   Education Level       1200000 non-null  object 
 7   Occupation            841925 non-null   object 
 8   Health Score          1125924 non-null  float64
 9   Location              1200000 non-null  object 
 10  Policy Type           1200000 non-null  object 
 11  Previous Claims       835971 non-null   float64
 12  Vehicle Age           1199994 non-null  float64
 13  Credit Score          1062118 non-null  float64
 14  Insurance Duration    1199999 non-null  float64
 15  Policy Start Date     1200000 non-null  object 
 16  Customer Feedback     1122176 non-null  object 
 17  Smoking Status        1200000 non-null  object 
 18  Exercise Frequency    1200000 non-null  object 
 19  Property Type         1200000 non-null  object 
 20  Premium Amount        1200000 non-null  float64
dtypes: float64(9), int64(1), object(11)
memory usage: 192.3+ MB

Key actionable insights:

Check Missing Values

# Missing Values Analysis 
print("\nMissing Values:\n")
missing_values = df.isnull().sum()
missing_percentage = (missing_values / len(df)) * 100
missing_df = pd.DataFrame({'Missing Values': missing_values, 'Percentage': missing_percentage})
print(missing_df[missing_df['Missing Values'] > 0].sort_values(by='Percentage', ascending=False))

Output:

                      Missing Values  Percentage
Previous Claims               364029   30.335750
Occupation                    358075   29.839583
Credit Score                  137882   11.490167
Number of Dependents          109672    9.139333
Customer Feedback              77824    6.485333
Health Score                   74076    6.173000
Annual Income                  44949    3.745750
Age                            18705    1.558750
Marital Status                 18529    1.544083
Vehicle Age                        6    0.000500
Insurance Duration                 1    0.000083

Key Actionable Insights:

Check the Distribution of Categorical Features

This step helps to:

# Identify Categorical Features
cat_features = df.select_dtypes(include=["object"]).columns.tolist()

# Remove 'Policy Start Date' if it exists (safe removal)
if "Policy Start Date" in cat_features:
    cat_features.remove("Policy Start Date")

# Calculate number of rows and columns for the subplots
n_cols = 3  # Number of columns
n_rows = math.ceil(len(cat_features) / n_cols)

# Create subplots
fig, axes = plt.subplots(n_rows, n_cols, figsize=(18, n_rows * 5))
axes = axes.flatten()  # Flatten in case of a single row

# Plot each categorical feature
for idx, col in enumerate(cat_features):
    ax = axes[idx]
    sns.countplot(data=df, x=col, ax=ax, order=df[col].value_counts().index)
    ax.set_title(f"Distribution of {col}")
    ax.set_xlabel(col)
    ax.set_ylabel("Count")
    ax.tick_params(axis='x', rotation=45)

# Hide any empty subplots
for i in range(len(cat_features), len(axes)):
    fig.delaxes(axes[i])

plt.tight_layout()
plt.show()

Output:

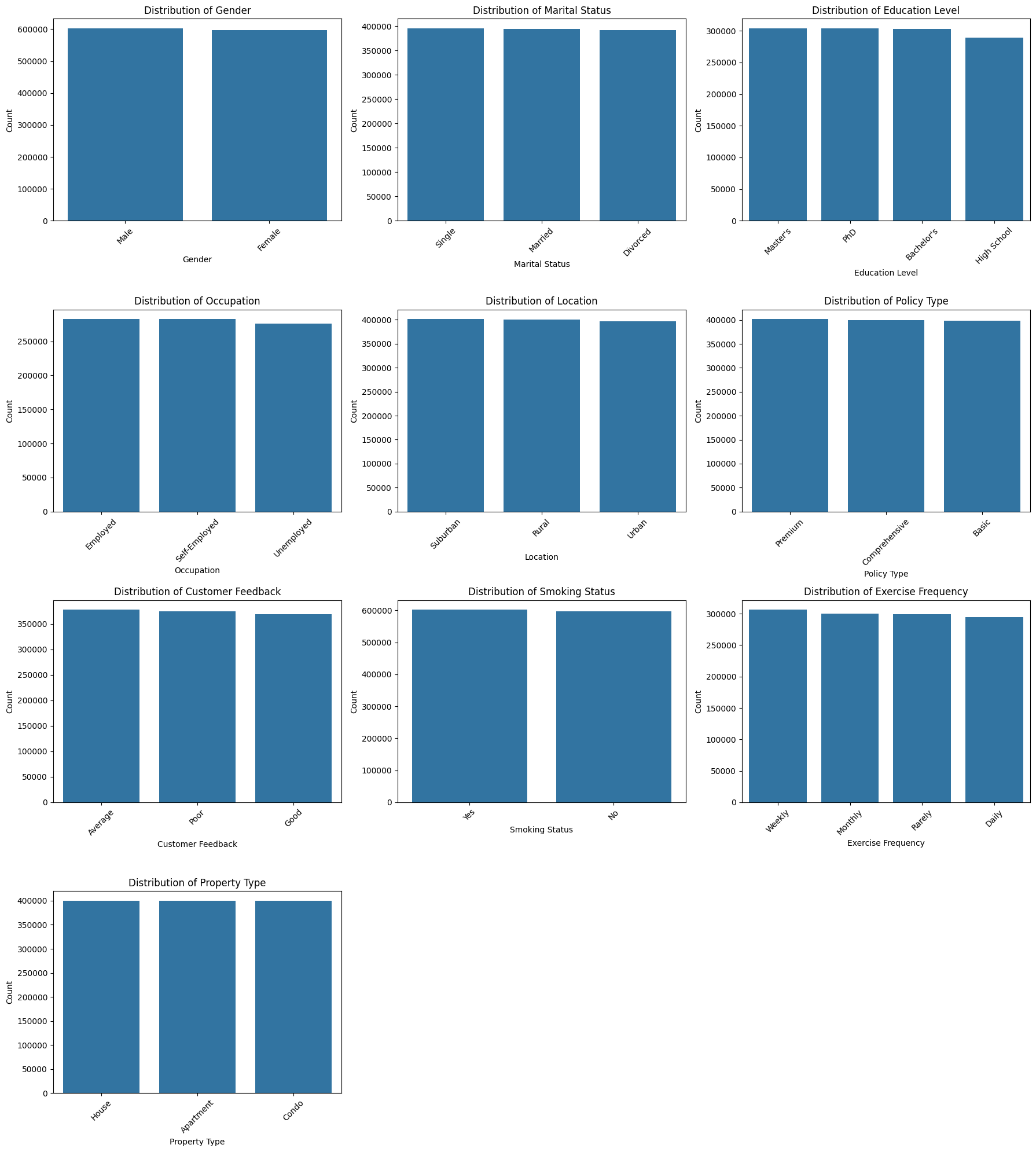
distribution

Key actionable insights

Check the Distribution and Boxplot of Numerical Features

This step helps to:

# Select Numerical Features
num_features = df.select_dtypes(include=["float64"]).columns.tolist()

# Remove the target if it's in the list
if "Premium Amount" in num_features:
    num_features.remove("Premium Amount")

# Plot all numerical features together
n_cols = 3  # number of columns of plots
n_rows = (len(num_features) + n_cols - 1) // n_cols  # calculate needed rows

plt.figure(figsize=(5 * n_cols, 4 * n_rows))

for idx, col in enumerate(num_features, 1):
    plt.subplot(n_rows, n_cols, idx)
    sns.histplot(df[col], kde=True, bins=30)
    plt.title(f"Distribution of {col}")
    plt.xlabel(col)
    plt.ylabel("Frequency")

plt.tight_layout()
plt.show()

Output:

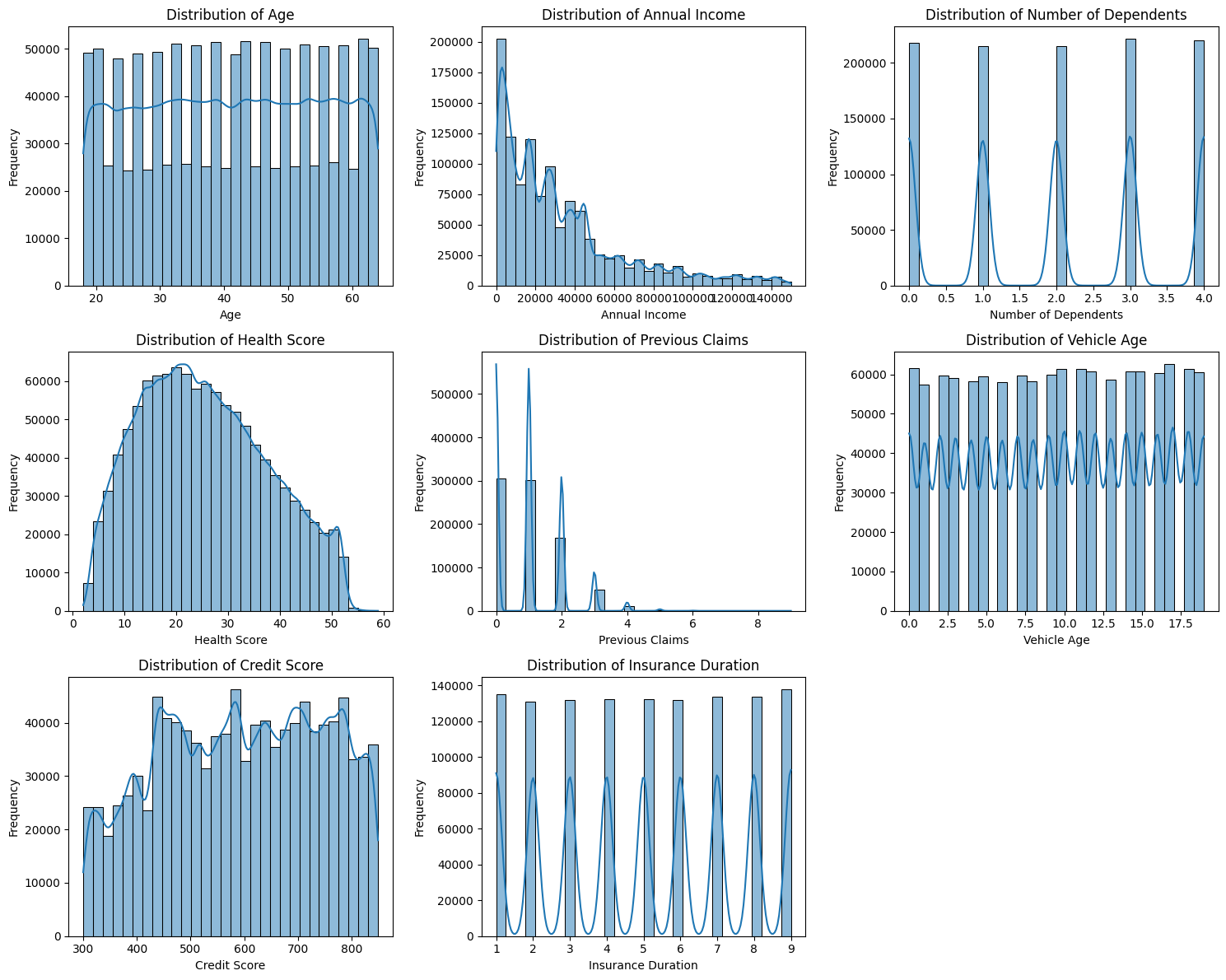
distribution

# Set up the plot grid
n_cols = 3  # Number of columns you want
n_rows = math.ceil(len(num_features) / n_cols)

fig, axes = plt.subplots(n_rows, n_cols, figsize=(18, n_rows * 4))  # Adjust figure size
axes = axes.flatten()

# Plot each numerical feature
for idx, col in enumerate(num_features):
    sns.boxplot(data=df, y=col, ax=axes[idx])
    axes[idx].set_title(f"Boxplot of {col}")

# Hide any empty subplots
for i in range(len(num_features), len(axes)):
    fig.delaxes(axes[i])

plt.tight_layout()
plt.show()

Output:

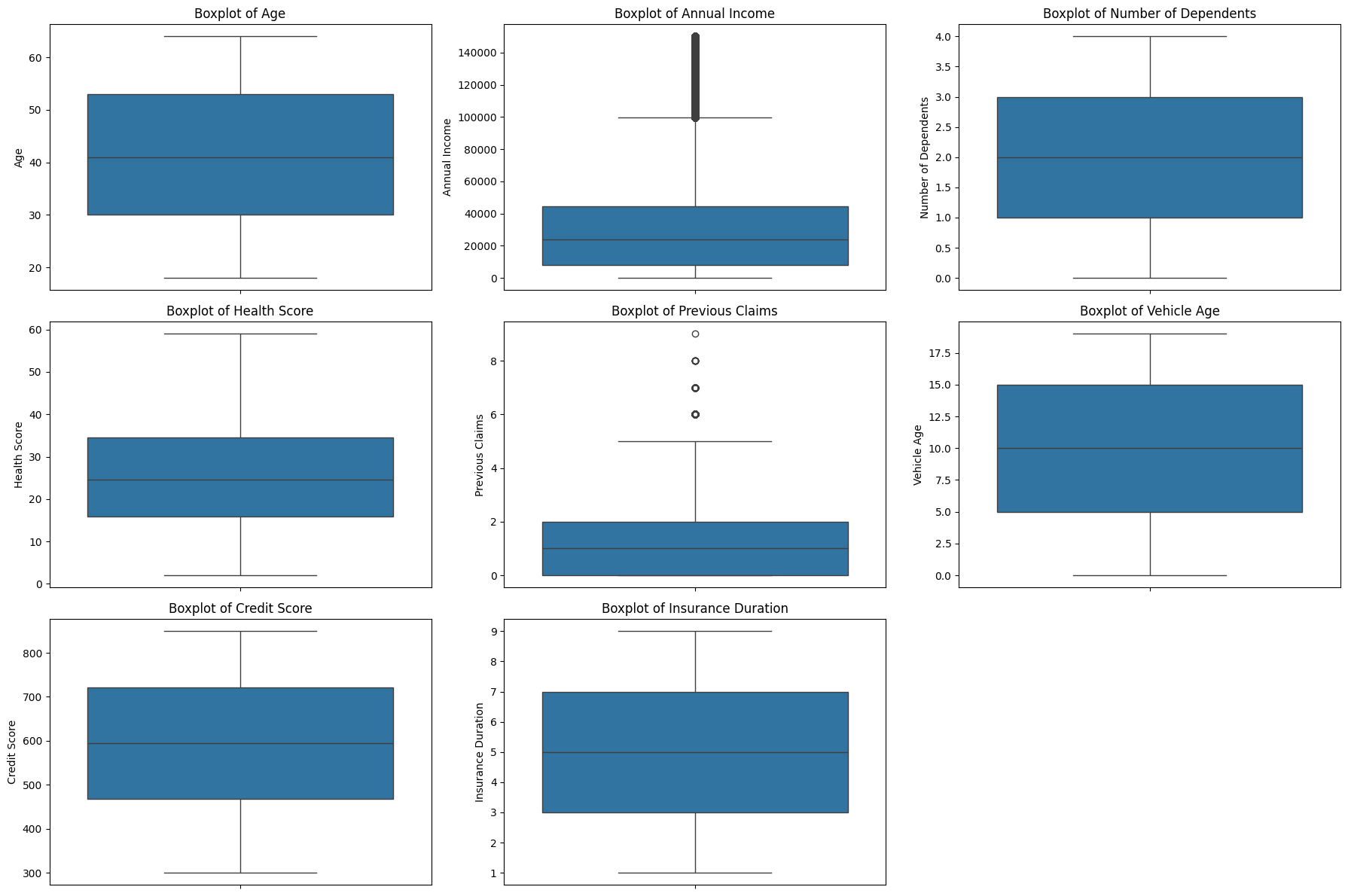
distribution

Key actionable insights

Check the Distribution and Boxplot of Target Variable (Premium Amount)

Checking the distribution and boxplot protects model performance by exposing skewness and outliers early.

# Distribution of Target Variable (Premium Amount)
plt.figure(figsize=(8, 5))
sns.histplot(df['Premium Amount'], bins=50, kde=True)
plt.title("Distribution of Premium Amount")
plt.xlabel("Premium Amount")
plt.ylabel("Frequency")
plt.show()

# Boxplot of Original Premium Amount
plt.figure(figsize=(8, 5))
sns.boxplot(x=df["Premium Amount"])
plt.title("Boxplot of Original Premium Amount")
plt.xlabel("Premium Amount")
plt.show()

Output:

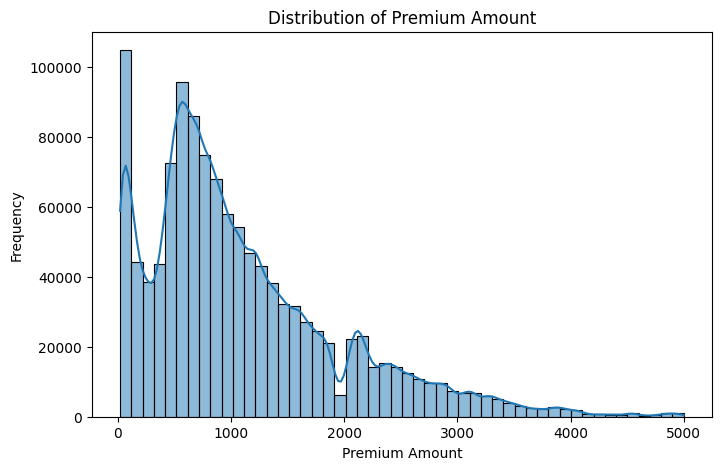
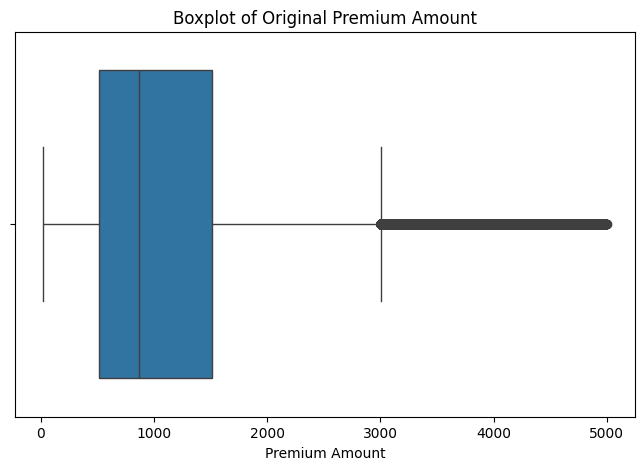
distribution

distribution

Key Actionable Insights:

Check for Multicollinearity Among Numerical Features using a Heatmap

# Correlation Matrix for Numerical Features
numeric_df = df.select_dtypes(include=['number'])

# Compute the correlation matrix
corr_matrix = numeric_df.corr()

# Plot the heatmap
plt.figure(figsize=(12, 8))
sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap="coolwarm", linewidths=0.5)
plt.title("Correlation Matrix of Numerical Features")
plt.show()

Output:

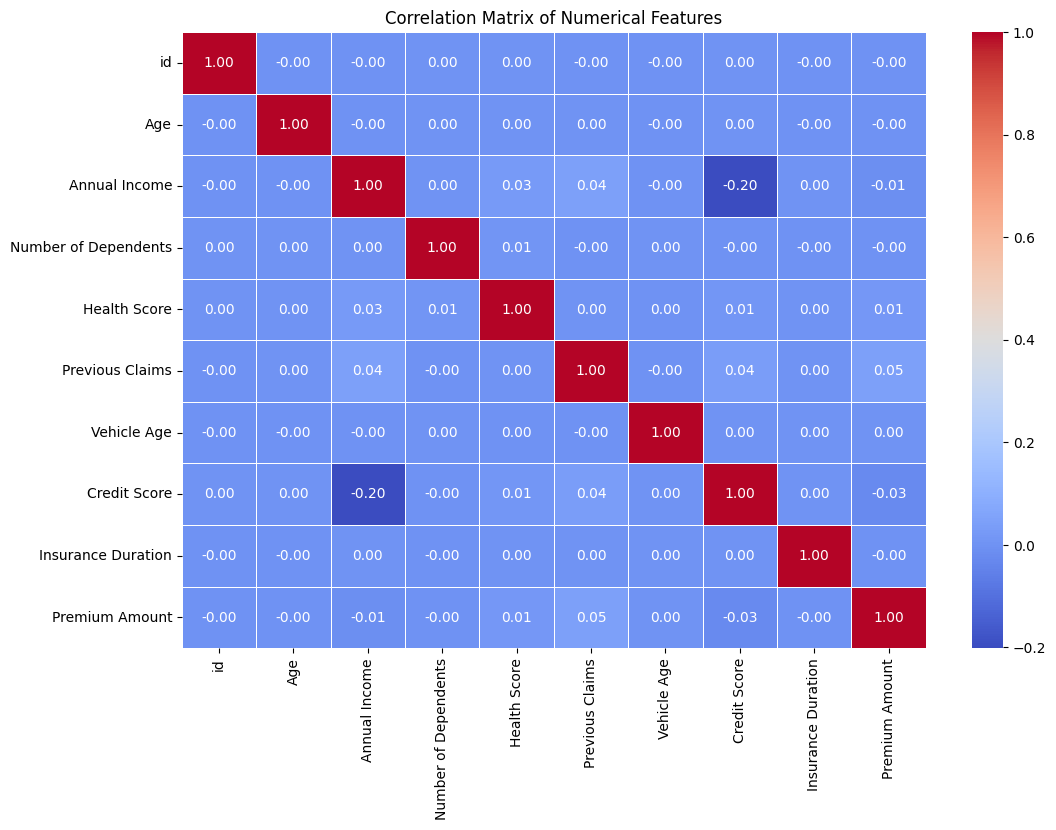
heatmap

Key Actionable Insights:

Check Dependencies between Categorical and Target Features

This step helps to:

Since Premium Amount is highly skewed, we use the Kruskal-Wallis H-test to test the dependency between categorical features and Premium Amount (instead of the commonly used ANOVA test with the assumption of normally distributed data).

cat_features = df.select_dtypes(include=["object"]).columns.tolist()

significance_level = 0.05

# Remove 'Policy Start Date' if exists
if "Policy Start Date" in cat_features:
    cat_features.remove("Policy Start Date")

# Store results
kruskal_results = {}

print("\n📊 Kruskal-Wallis H-test Results (Categorical Features vs Target - Premium Amount):")
print("=" * 60)

for cat_col in cat_features:
    # Prepare groups
    groups = [df["Premium Amount"][df[cat_col] == category] for category in df[cat_col].dropna().unique()]
    
    # Check if there are at least 2 groups with data
    if len(groups) > 1:
        stat, p_value = kruskal(*groups)
        kruskal_results[cat_col] = p_value
        
        if p_value < significance_level:
            print(f"✔ {cat_col} vs Premium Amount | p-value: {p_value:.6f} (Significant ✅)")
        else:
            print(f"❌ {cat_col} vs Premium Amount | p-value: {p_value:.6f} (Not Significant)")

Output:

📊 Kruskal-Wallis H-test Results (Categorical Features vs Target - Premium Amount):
============================================================
❌ Gender vs Premium Amount | p-value: 0.893486 (Not Significant)
❌ Marital Status vs Premium Amount | p-value: 0.557764 (Not Significant)
❌ Education Level vs Premium Amount | p-value: 0.283390 (Not Significant)
✔ Occupation vs Premium Amount | p-value: 0.043357 (Significant ✅)
❌ Location vs Premium Amount | p-value: 0.179990 (Not Significant)
❌ Policy Type vs Premium Amount | p-value: 0.385302 (Not Significant)
❌ Customer Feedback vs Premium Amount | p-value: 0.110280 (Not Significant)
❌ Smoking Status vs Premium Amount | p-value: 0.680346 (Not Significant)
❌ Exercise Frequency vs Premium Amount | p-value: 0.430723 (Not Significant)
❌ Property Type vs Premium Amount | p-value: 0.419278 (Not Significant)

Key Actionable Insights:

Action Points from EDA

4 . Data Preprocessing

Feature engineering:

From Policy Start Date, we extract the useful following features that allow the model to capture hidden temporal patterns:

We also remove the unnecessary columns:

# Convert Date Features
df["Policy Start Date"] = pd.to_datetime(df["Policy Start Date"])
df["year"] = df["Policy Start Date"].dt.year.astype("float32")
df["month"] = df["Policy Start Date"].dt.month.astype("float32")
df["day"] = df["Policy Start Date"].dt.day.astype("float32")
df["dow"] = df["Policy Start Date"].dt.dayofweek.astype("float32")
df.drop(columns=["Policy Start Date", "id"], inplace=True, errors="ignore")  # Remove ID and date column

Log Transformation for the Target Feature

Since the distribution of Premium Amount is highly skewed, we will use a log transformation for the data preprocessing step.

This transformation helps models like Ridge, Lasso, LightGBM, XGBoost work better with:

# Identify Categorical & Numerical Features
cat_features = df.select_dtypes(include=["object"]).columns.tolist()
num_features = df.select_dtypes(include=["float64"]).columns.tolist()

# Define Target Variable (Log Transformation to Reduce Skewness)
df["Premium Amount"] = np.log1p(df["Premium Amount"])  # log(1 + x) transformation
num_features.remove("Premium Amount")  # Exclude target variable

Check again the distribution and boxplot of the log-transformed premium amount

# Distribution of Transformed Target Variable (Premium Amount)
plt.figure(figsize=(8, 5))
sns.histplot(df['Premium Amount'], bins=50, kde=True)
plt.title("Distribution of Log-Transformed Premium Amount")
plt.xlabel("Log-Transformed Premium Amount")
plt.ylabel("Frequency")
plt.show()

# Boxplot of Log-Transformed Premium Amount
plt.figure(figsize=(8, 5))
sns.boxplot(x=df["Premium Amount"])
plt.title("Boxplot of Log-Transformed Premium Amount")
plt.xlabel("Premium Amount")
plt.show()

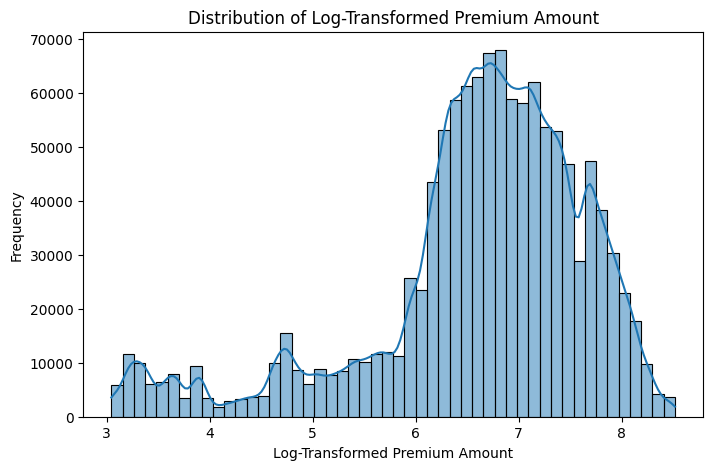
distribution log transformed

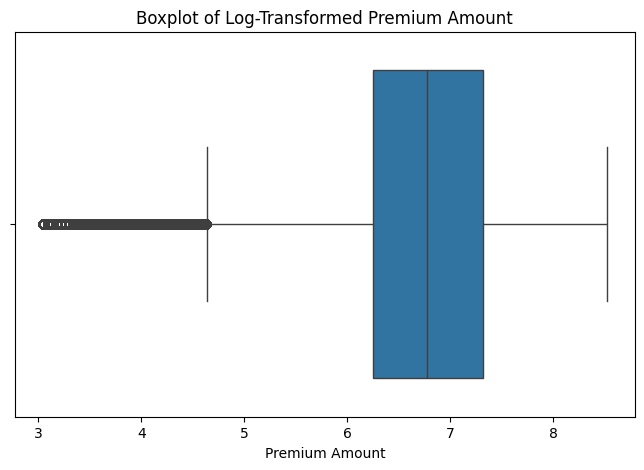
distribution

After the log transformation, the data is now closer to a normal (Gaussian-like) distribution.

5. Model Selection and Training

From the insights from the EDA step, we will use XGBoost for the best predictive model choice because it minimizes preprocessing needs while maximizing robustness and predictive performance.

Key Steps:

# Convert Categorical Features to "category" dtype for XGBoost
for col in cat_features:
    df[col] = df[col].astype("category")

# Define Features and Target
X = df.drop(columns=["Premium Amount"])
y = df["Premium Amount"]

# Cross-Validation Setup (5-Fold)
kf = KFold(n_splits=5, shuffle=True, random_state=42)
oof_preds = np.zeros(len(X))  # Out-of-Fold Predictions
feature_importance_df = pd.DataFrame(index=X.columns)
rmsle_per_fold = []  # Store RMSLE per fold

# Train XGBoost with Cross-Validation
for fold, (train_idx, valid_idx) in enumerate(kf.split(X)):
    print(f"🚀 Training Fold {fold + 1}...")

    # Split Data
    X_train, X_valid = X.iloc[train_idx], X.iloc[valid_idx]
    y_train, y_valid = y.iloc[train_idx], y.iloc[valid_idx]

    # Train XGBoost Model with Native Categorical Handling
    model = XGBRegressor(
        enable_categorical=True,
        tree_method="hist",  # Optimized for speed
        max_depth=8,
        learning_rate=0.01,
        n_estimators=2000,
        colsample_bytree=0.9,
        subsample=0.9,
        early_stopping_rounds=50,
        eval_metric="rmse",
        random_state=42
    )
    model.fit(
        X_train, y_train,
        eval_set=[(X_valid, y_valid)],
        verbose=100
    )

    # Out-of-Fold Predictions
    fold_preds = model.predict(X_valid)
    oof_preds[valid_idx] = fold_preds

    # Calculate RMSLE for This Fold
    fold_rmsle = np.sqrt(mean_squared_log_error(np.expm1(y_valid), np.expm1(fold_preds)))
    rmsle_per_fold.append(fold_rmsle)
    print(f"✔ Fold {fold + 1} RMSLE: {fold_rmsle:.5f}")

    # Store Feature Importance
    feature_importance_df[f"Fold_{fold + 1}"] = model.feature_importances_

Output:

🚀 Training Fold 1...
[0]	validation_0-rmse:1.09602
[100]	validation_0-rmse:1.05936
[200]	validation_0-rmse:1.04985
[300]	validation_0-rmse:1.04745
[400]	validation_0-rmse:1.04674
[500]	validation_0-rmse:1.04652
[600]	validation_0-rmse:1.04640
[700]	validation_0-rmse:1.04635
[800]	validation_0-rmse:1.04631
[900]	validation_0-rmse:1.04630
[1000]	validation_0-rmse:1.04628
[1100]	validation_0-rmse:1.04628
[1116]	validation_0-rmse:1.04627
✔ Fold 1 RMSLE: 1.04627
🚀 Training Fold 2...
[0]	validation_0-rmse:1.09482
[100]	validation_0-rmse:1.05816
[200]	validation_0-rmse:1.04877
[300]	validation_0-rmse:1.04647
[400]	validation_0-rmse:1.04584
[500]	validation_0-rmse:1.04566
[600]	validation_0-rmse:1.04561
[700]	validation_0-rmse:1.04558
[771]	validation_0-rmse:1.04558
✔ Fold 2 RMSLE: 1.04557
🚀 Training Fold 3...
[0]	validation_0-rmse:1.09471
[100]	validation_0-rmse:1.05882
[200]	validation_0-rmse:1.04953
[300]	validation_0-rmse:1.04726
[400]	validation_0-rmse:1.04661
[500]	validation_0-rmse:1.04644
[600]	validation_0-rmse:1.04636
[700]	validation_0-rmse:1.04633
[800]	validation_0-rmse:1.04631
[900]	validation_0-rmse:1.04630
[950]	validation_0-rmse:1.04630
✔ Fold 3 RMSLE: 1.04630
🚀 Training Fold 4...
[0]	validation_0-rmse:1.09521
[100]	validation_0-rmse:1.05785
[200]	validation_0-rmse:1.04809
[300]	validation_0-rmse:1.04553
[400]	validation_0-rmse:1.04480
[500]	validation_0-rmse:1.04457
[600]	validation_0-rmse:1.04448
[700]	validation_0-rmse:1.04442
[800]	validation_0-rmse:1.04441
[900]	validation_0-rmse:1.04440
[1000]	validation_0-rmse:1.04438
[1100]	validation_0-rmse:1.04436
[1140]	validation_0-rmse:1.04438
✔ Fold 4 RMSLE: 1.04436
🚀 Training Fold 5...
[0]	validation_0-rmse:1.09641
[100]	validation_0-rmse:1.05924
[200]	validation_0-rmse:1.04941
[300]	validation_0-rmse:1.04689
[400]	validation_0-rmse:1.04616
[500]	validation_0-rmse:1.04592
[600]	validation_0-rmse:1.04583
[700]	validation_0-rmse:1.04577
[800]	validation_0-rmse:1.04574
[900]	validation_0-rmse:1.04572
[929]	validation_0-rmse:1.04572
✔ Fold 5 RMSLE: 1.04571

6. Model Evaluation

We evaluated models using:

# Compute and Print Overall RMSLE
overall_rmsle = np.mean(rmsle_per_fold)
print("\n📊 Cross-Validation RMSLE Scores per Fold:")
for i, score in enumerate(rmsle_per_fold):
    print(f"✔ Fold {i + 1} RMSLE: {score:.5f}")
print(f"\n🚀 Overall Cross-Validation RMSLE: {overall_rmsle:.5f}")

# Compute Final RMSLE Using All Out-of-Fold Predictions
final_rmsle = np.sqrt(mean_squared_log_error(np.expm1(y), np.expm1(oof_preds)))
print(f"\n✅ Final Model RMSLE: {final_rmsle:.5f}")

Output:

📊 Cross-Validation RMSLE Scores per Fold:
✔ Fold 1 RMSLE: 1.04627
✔ Fold 2 RMSLE: 1.04557
✔ Fold 3 RMSLE: 1.04630
✔ Fold 4 RMSLE: 1.04436
✔ Fold 5 RMSLE: 1.04571

🚀 Overall Cross-Validation RMSLE: 1.04564

✅ Final Model RMSLE: 1.04564

# Compute Average Feature Importance
feature_importance_df["Average"] = feature_importance_df.mean(axis=1)
feature_importance_df = feature_importance_df.sort_values(by="Average", ascending=False)

# Plot Top 20 Important Features
plt.figure(figsize=(12, 6))
sns.barplot(
    x=feature_importance_df["Average"][:20], 
    y=feature_importance_df.index[:20], 
    palette="viridis"
)
plt.xlabel("Feature Importance Score")
plt.ylabel("Features")
plt.title("Top 20 Important Features")
plt.show()

Output:

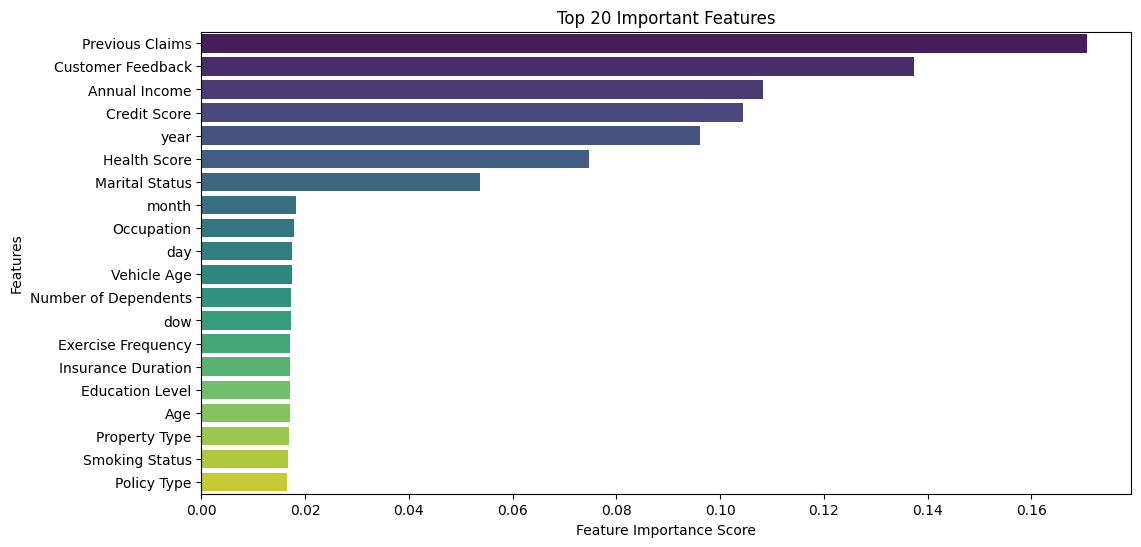
feature imporatant

Key Actionable Insights:

Next steps for improvements

To further enhance this insurance premium prediction project, the potential future steps are:

  1. Build Scalable and Automated Data Pipelines:
    • Develop automated end-to-end pipelines by combining SQL for data extraction, Apache Airflow for scheduling and orchestration, and Databricks for collaborative data engineering and machine learning development at scale. (Focus: orchestrating and automating workflows across systems.)
  2. Improve Project Structure and Maintainability
    • Use Kedro to structure the project into modular, reproducible, and maintainable pipelines. This ensures that as the project grows, it remains clean, easy to extend, and production-ready. (Focus: clean codebase design and reproducibility.)
  3. Accelerate Large-Scale Data Processing and Modeling
    • Use Dask / RAPIDS to boost the speed of data processing and model training by using Dask for distributed parallel computing and RAPIDS for GPU-accelerated machine learning, enabling efficient handling of very large datasets. (Focus: computational performance and scalability.)
  4. Productionize the Model with Containers and Cloud
    • Use Docker to package the model and its dependencies into a Docker container and deploy it on Kubernetes for scalable, reliable production serving.
    • Use Cloud Platforms (AWS, GCP, Azure) to deploy the solution in the cloud using services like AWS SageMaker, GCP Vertex AI, or Azure ML for robust training, deployment, and monitoring in production environments.
  5. Further Enhancements for Model Quality and Reliability
    • Perform large-scale hyperparameter tuning using frameworks like Optuna or Ray Tune.
    • Add advanced model explainability using tools like SHAP or LIME to build stakeholder trust.
    • Set up real-time monitoring dashboards to track model drift, prediction quality, and data pipeline health over time.

Conclusion

This project successfully built a data-driven insurance premium prediction model using EDA, feature engineering, and XGBoost. Our model mimics the insurer’s pricing approach, revealing key premium factors while improving transparency.

The code of this project is available here.

For further inquiries or collaboration, please contact me at my email.